Esercitazione 5

Domande a risposta multipla

2025-01-08, domanda 1

Il fatto che il risultato di una IMUL non sta sul numero di bit dove la IMUL intende scriverlo:

1. È rilevato da un'eccezione.
2. È indicato dal fatto che OF va ad 1.
3. È indicato dal fatto che CF va ad 1.
4. Nessuna delle precedenti.

Risposta

La risposta giusta è la d.

Una moltiplicazione tra due naturali su $n$ bit sta su $2n$ bit. Una IMUL a $n$ bit scrive il suo risultato su uno o più registri per un totale di $2n$ bit. Quindi la IMUL non può mai avere problemi nella scrittura del risultato, e non comunica questo con nessun flag.

I flag CF e OF sono invece settati se il risultato non è riducibile su $n$ bit.

2025-01-08, domanda 2

Un sommatore ad una cifra in base 10 BCD può essere realizzato concatenando 4 full adder in base 2 in montaggio ripple carry.

1. Vero, sia per naturali che per interi.
2. Vero, ma solo per naturali.
3. Falso.
4. Nessuna delle precedenti.

Risposta

La risposta giusta è la c.

Un sommatore in base 10 deve considerare cifre da $0$ a $9$, mentre concatenando 4 full adder in base 2 si ottiene un sommatore a 4 cifre in base 2, che considera risultati da $0$ a $15$. Come esempio della differenza, si prenda la somma $7 + 7$, che in base 2 è 0b0111 + 0b0111. In base 10, ci aspettiamo il risultato $4$ con riporto di $1$, mentre con il sommatore di cui sopra otteniamo $0b1110$ con riporto $0$. Similmente, provare la somma $-1 + (-1)$ per un controesempio con numeri interi.

2025-01-08, domanda 4

Affinché la divisione intera tra $a$ (dividendo) e $b$ (divisore) abbia un quoziente rappresentabile sul numero di cifre richiesto, il fatto che lo abbia la divisione naturale tra $|a|$ e $|b|$ è condizione:

1. Sufficiente.
2. Necessaria.
3. Necessaria e sufficiente.
4. Nessuna delle precedenti.

Risposta

La risposta giusta è la b.

L'affermazione deriva direttamente dalla discussione in sezione 4.8.4 delle dispense sull'aritmetica. Per eseguire la divisione per interi si può riutilizzare la circuiteria per la divisione tra naturali, sotto le ipotesi

$$\begin{cases} |r| \lt |b| \\ sgn(r) = sgn(a), \end{cases}$$

che ci permettono di scrivere $|a| = |q| \cdot |b| + |r|$. Se questa divisione tra naturali non è fattibile, significa che il naturale $|q|$ non è rappresentabile su $n$ bit, e quindi neanche l'intero $q$ potrà essere rappresentabile su $n$ bit. La condizione non è però sufficiente: non è detto che se $|q|$ fosse rappresentabile su $n$ bit allora anche $q$ lo sarebbe.

2025-01-08, domanda 5

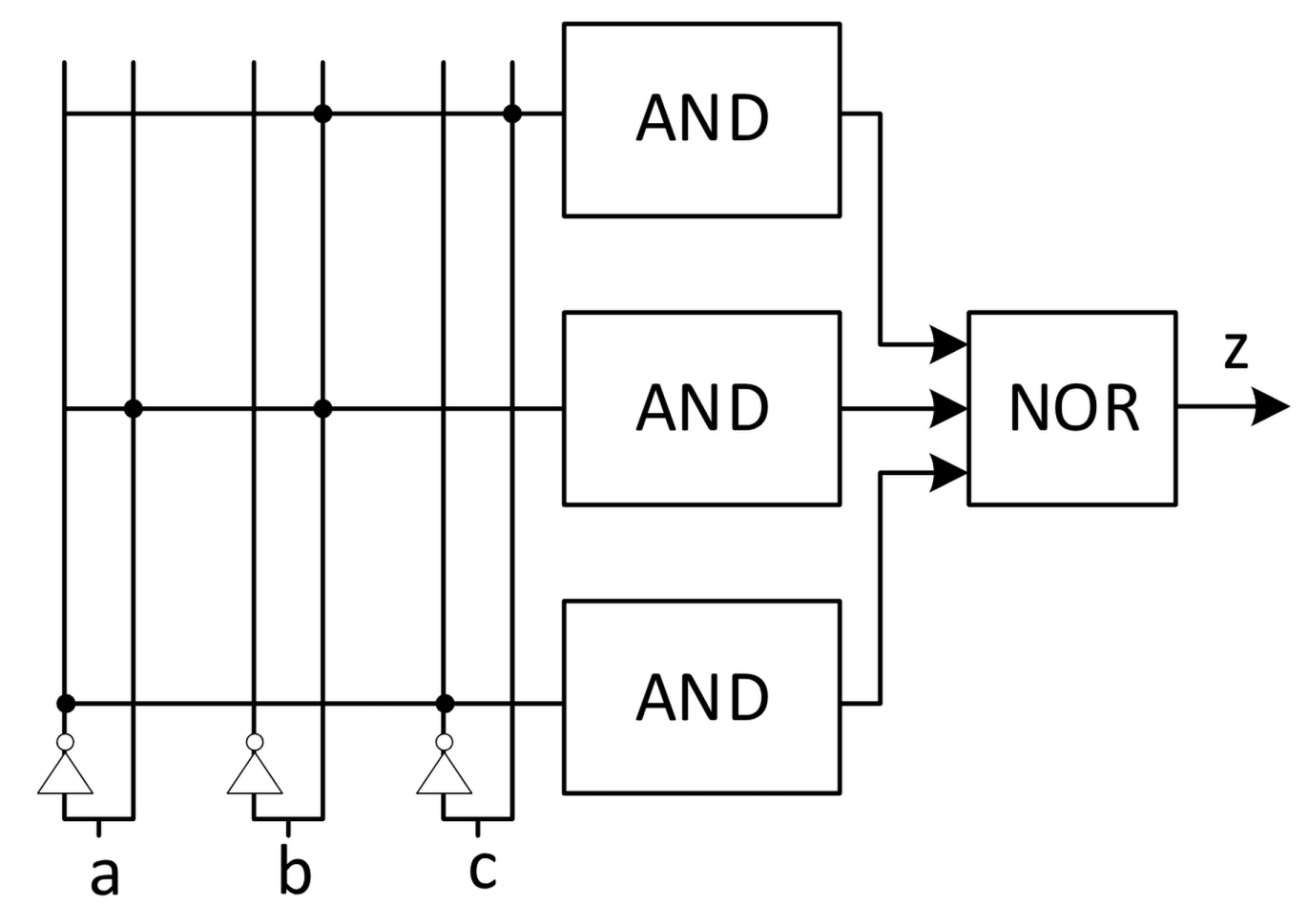
La rete disegnata di sopra riconosce un numero di stati di ingresso pari a:

1. 6
2. 4
3. 3
4. Nessuna delle precedenti.

Risposta

La risposta giusta è la c.

Per un esercizio del genere si hanno, in generale, due approcci: la compilazione esaustiva della tabella di verità, o lo sviluppo algebrico. Qui le indico entrambe.

Tabella di verità. Dato che abbiamo 3 ingressi, dovremmo compilare una tabella di $2^3 = 8$ righe. Ci possiamo aiutare con l'aggiunta di colonne intermedie per il primo livello di logica.

$a$	$b$	$c$	$\overline{a} \cdot \overline{c}$	$a \cdot b$	$b \cdot c$	$\overline{ (\overline{a} \cdot \overline{c}) + (a \cdot b) + (b \cdot c)}$
0	0	0	1	0	0	0
0	0	1	0	0	0	1
0	1	0	1	0	0	0
0	1	1	0	0	1	0
1	0	0	0	0	0	1
1	0	1	0	0	0	1
1	1	0	0	1	0	0
1	1	1	0	1	1	0

Sono tre le righe dove otteniamo 1 come risultato.

Sviluppo algebrico. Cominciamo riscrivendo la figura di sopra come espressione booleana: $\overline{ (\overline{a} \cdot \overline{c}) + (a \cdot b) + (b \cdot c)}$.

Sviluppiamo l'espressione utilizzando le leggi di De Morgan: $\overline{x + y} = \overline{x} \cdot \overline{y}$, $\overline{x \cdot y} = \overline{x} + \overline{y}$.

$$\begin{align*} \overline{ (\overline{a} \cdot \overline{c}) + (a \cdot b) + (b \cdot c)} &= \overline{\overline{a} \cdot \overline{c}} \cdot \overline{a \cdot b} \cdot \overline{b \cdot c} \\ &= (a + c) \cdot (\overline{a} + \overline{b}) \cdot (\overline{b} + \overline{c}) \\ \end{align*}$$

Ora possiamo espanderla utilizzando la proprietà distributiva $(x + y) \cdot z = (x \cdot z) + (y \cdot z)$. Nel far questo, ricordiamo che $x \cdot \overline{x} = 0$, $x \cdot x = x$ e $(x \cdot y) + x = x \cdot (y + 1) = x$.

$$\begin{align*} (a + c) \cdot (\overline{a} + \overline{b}) \cdot (\overline{b} + \overline{c}) &= a \cdot (\overline{a} + \overline{b}) \cdot (\overline{b} + \overline{c}) + c \cdot (\overline{a} + \overline{b}) \cdot (\overline{b} + \overline{c}) \\ &= \cancel{ a \cdot \overline{a} \cdot (\overline{b} + \overline{c}) } + a \cdot \overline{b} \cdot (\overline{b} + \overline{c}) + c \cdot (\overline{a} + \overline{b}) \cdot \overline{b} + \cancel{ c \cdot (\overline{a} + \overline{b}) \cdot \overline{c} } \\ &= a \cdot \overline{b} \cdot \cancel{ \overline{b} } + a \cdot \overline{b} \cdot \overline{c} + c \cdot \overline{a} \cdot \overline{b} + c \cdot \overline{b} \cdot \cancel{ \overline{b} } \\ &= (a + c) \cdot \overline{b} \end{align*}$$

Da quest'ultima espressione si ha che gli stati riconosciuti sono tutti e solo quelli con $b = 0$ e almeno uno tra $a$ e $c$ a 1. Questi sono tre, ossia $\{a, b, c\} = 001; 100; 101$.

2025-01-08, domanda 9

In complemento alla radice in base $\beta = 14$ su una cifra, la rappresentazione dell'intero $-8$:

1. È codificata come 1000.
2. È codificata come 1010.
3. È codificata come 0110.
4. Nessuna delle precedenti.

Risposta

La risposta giusta è la d.

In complemento alla radice in una base $\beta$ su $n$ cifre, possiamo rappresentare numeri interi nell'intervallo $[-\lfloor \frac{\beta^n}{2} \rfloor, \lfloor \frac{\beta^n}{2} \rfloor - 1 ]$. Nelle condizioni di questa domanda, tale intervallo è $[-7, 6]$. Dato che tale intervallo non comprende $-8$, questo numero non è rappresentabile.